5.1. Когда была изобретена позиционная система счисления?
Сегодня считается, что позиционная система записи чисел была изобретена в Индии «очень давно» [821], с. 88. И затем заимствована арабами, которые наконец-то и принесли ее в средневековую Европу. Именно в Европе «арабские цифры» послужили толчком к быстрому развитию математики и вычислений во второй половине XVI — начале XVII века В 1585 году были уже изобретены десятичные дроби [821], с 119. Историк математики Д. Л. Стройк пишет: «Это было одним из больших усовершенствований, которые стали возможными благодаря всеобщему принятию индийско-арабской системы счисления. Другим большим усовершенствованием вычислительной техники было изобретение логарифмов» [821], с. 120. Напомним, что логарифмы были изобретены в первой половине XVII века [821], с. 120–121.
Подчеркнем, что как десятичные дроби, так и логарифмы могли появиться лишь ПОСЛЕ ВВЕДЕНИЯ ПОЗИЦИОННОЙ ДЕСЯТИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ. Причем ВСКОРЕ после, поскольку, коль скоро позиционная система счисления была внедрена, изобретение дробей и логарифмов уже не заключало в себе особой сложности. В самом деле, рассмотрим вопрос об изобретении десятичных дробей. Если мы имеем позиционную систему счисления, то перемещение любой цифры на один разряд вверх «повышает ее вес», то есть вклад этой цифры в значение записанного в позиционной системе числа, в десять раз. Для целых чисел самым младшим разрядом является разряд единиц. Естественная мысль — добавить разряды «ниже» разряда единиц по тому же правилу: перемещение цифры на разряд вниз уменьшает ее вклад в результирующее значение в десять раз. Для того чтобы сделать это, достаточно придумать разделитель целых и дробных разрядов. То есть десятичную запятую. Например, в записи числа 16, 234 запятая отделяет два целых разряда от трех дробных. Вряд ли для такого изобретения потребовались СОТНИ лет, как на том настаивает скалигеровская история науки. Скорее всего, это было сделано довольно быстро, за десятки лет, вскоре после изобретения нуля и позиционной системы счисления.
Чуть более сложным, но тоже не представляющим из себя принципиальных затруднений является изобретение ДЕСЯТИЧНЫХ ЛОГАРИФМОВ — опять-таки на основе десятичной позиционной системы счисления. Дело в том, что целая часть десятичного логарифма это ДЛИНА ЗАПИСИ ЧИСЛА в позиционной десятичной системе, уменьшенная на единицу. Не трудно заметить — и это, скорее всего, было достаточно быстро сделано, — что при умножении двух натуральных чисел длины их записей в общем-то складываются (с точностью до единицы, которую иногда приходится вычитать). Последнее связано с тем, что при умножении чисел их логарифмы складываются, следовательно, целые части логарифмов тоже складываются с точностью до единицы. Лишняя единица возникает тогда, когда сумма дробных частей складываемых логарифмов больше или равна единице. Естественная задача для средневекового математика — уточнить характеристику, задаваемую длиной числа, таким образом, чтобы при перемножении чисел эти характеристики В ТОЧНОСТИ СКЛАДЫВАЛИСЬ. Правильное понимание идеи мгновенно приводит к понятию логарифма. Именно эту задачу и пытался решить Джон Непер при создании логарифмов в начале XVII века. Он придумал логарифмы. Сначала в несколько неуклюжей форме, но затем идея была быстро доведена до ее почти современного состояния [821], с 121. Д. Я. Стройк сообщает, что полная таблица десятичных логарифмов целых чисел от единицы до ста тысяч была опубликована в 1627 году [821], с. 121. То есть всего лишь через 13 лет после первой работы Джона Непера на эту тему [821], с 120–121.
Следовательно, от появления идеи позиционного десятичного счисления до создания десятичных дробей и логарифмов не могло пройти очень много времени. А поскольку логарифмы были созданы лишь в начале XVII века, то можно уверенно предположить, что распространение позиционной десятичной системы счисления началось НЕ РАНЕЕ СЕРЕДИНЫ XVI ВЕКА Н. Э. Причем на первых порах — среди математиков и вычислителей, то есть представителей сравнительно узкого круга ученых. И лишь затем эта идея проникла в общество, и ею стали пользоваться издатели, художники, школьные учителя и та
Но сегодня нас хотят убедить, что в западноевропейском обществе такие далекие от математики люди, как, например, художники, свободно пользовались позиционной десятичной системой счисления уже в XV веке и даже в более ранние эпохи. Не говоря уж об индусах, которые якобы пользовались этой системой аж в 500 году до н. э. (!) [755], с. 20. Правда, как потом рассказывает нам та же скалигеровская история науки, «древние» индусы почему-то «забыли» об этих своих выдающихся математических открытиях. Но, по счастью, успели рассказать о них арабам. Которые и донесли этот светоч «древнейших знаний» до необразованной Европы. Произошло это в Средние века. Индия в это время (как, впрочем, и Европа) была погружена в мрачную эпоху средневекового невежества. По крайней мере математического. Во всяком случае, как нам говорят сегодня, «относительно математики в Китае и в Индии мы располагаем очень ограниченным запасом сведений. Либо исчезли, ЛИБО ЕЩЕ НЕ НАЙДЕНЫ многие материальные свидетельства» [755], с. 45.
По нашему мнению, нарисованная историками картина неестественна и даже нелепа. Определить примерную дату изобретения позиционной десятичной системы счисления можно по бурному развитию и внедрению этой идеи, которое началось лишь в конце XVI века [821]. Следовательно, сама идея возникла где-то в середине XVI века, а не в глубокой древности. Нельзя отделять идею от ее прямых и ОЧЕВИДНЫХ следствий СОТНЯМИ и даже ТЫСЯЧАМИ лет. Поэтому все те «древне»-вавилонские, «древне»-индийские, «древне»-арабские и вообще «очень-очень древние» тексты, в которых использована идея позиционного десятичного счисления, не могли появиться ранее XVI века.
Это в полной мере относится и к якобы «древнейшей» КЛИНОПИСИ Двуречья. Сегодня нам говорят, будто «древние шумеры» еще в ТРЕТЬЕМ ТЫСЯЧЕЛЕТИИ ДО Н.Э. широко пользовались позиционной системой [821], с. 40. А якобы за ДВЕ ТЫСЯЧИ ЛЕТ ДО Н.Э. они уже свободно решают линейные и квадратные уравнения с двумя неизвестными. Д. Л. Стройк сообщает: «Вавилоняне времен Хаммурапи ПОЛНОСТЬЮ владели техникой решения квадратных уравнений. Они решали линейные и квадратные уравнения с двумя неизвестными, решали даже задачи, сводящиеся к кубическим и биквадратным уравнениям» 1821], с. 42. А В ПЕРВОМ ТЫСЯЧЕЛЕТИИ ДО Н.Э. «древние шумеры» производят вычисления «которые доведены до СЕМНАДЦАТОГО шестидесятичного знака. СТОЛЬ СЛОЖНЫЕ ВЫЧИСЛИТЕЛЬНЫЕ работ уже нельзя связывать с вычислением налогов или измерением, — стимулом для них были астрономические задачи» [821], с. 44.
По нашему мнению, все эти «древне»-шумерские математические высоты были достигнуты лишь в XVI–XVII или даже в ВОСЕМНАДЦАТОМ веках НАШЕЙ ЭРЫ. А отнюдь не до нашей эры, как полагают историки, основываясь на ошибочной хронологии Скалигера. Недаром даже Джон Непер, изобретатель логарифмов, «избегал операций с дробями» [755], с. 130. Хотя историки математики считают, что он производил действия с дробями «легко», тем не менее, сам факт избегания дробей весьма красноречив. И неудивителен. Поскольку, как мы видели, десятичные ДРОБИ были изобретены лишь в 1585 году, когда Джону Неперу (1550–1617) было уже 35 лет [821], с 121. А до этого операции с дробями были громоздки и неудобны. Математики, бухгалтеры, счетоводы, астрономы XVI–XVIII веков нашей эры, жившие на территории Междуречья, по-видимому, еще не имели в достаточном количестве бумаги. Поэтому были вынуждены записывать свои вычисления на глиняных табличках. Которые быстро вышли из употребления в XVIII–XIX веках, когда здесь наконец-то появилась бумага в достаточном количестве. Затем, лет через сто, радостно заброшенные таблички были обнаружены западноевропейскими археологами. И тут же с восторгом объявлены «древнейшим свидетельством могущества допотопной шумерской науки». Расцветшей якобы в III тысячелетии до н. э. Местные жители возражать не стали.
5.2. Как появились арабские цифры для позиционной записи чисел?
Д. Л. Стройк пишет: «Весьма разнообразны знаки, которые применялись для записи цифр в позиционной системе, но имеются два главных типа: индийские обозначения, которые применялись восточными арабами, и так называемые цифры „гобар“ (или „губар“), которые применялись западными арабами в Испании. Знаки первого типа и сейчас еще применяются в арабском мире, но наша современная система, по-видимому произошла из системы „гобар“» [821], с. 89.
ВОПРОС О ПРОИСХОЖДЕНИИ «АРАБСКИХ ЦИФР» ОСТАЕТСЯ В СКАЛИГЕРОВСКОЙ ИСТОРИИ НАУКИ ОТКРЫТЫМ ДО СИХ ПОР. Существуют различные теории на этот счет. Например, теория Вепке, согласно которой арабские цифры проникли на Запад якобы в V веке из Александрии через неопифагорейцев [821], с. 90. Есть и другая теория — Н. М. Бубнова. Согласно ей, знаки «гобар» произошли из давних римско-греческих символов [821], с. 90. Но ни в том, ни в другом случае не предъявляются РОДОНАЧАЛЬНИКИ хорошо знакомых нам арабских цифр. В качестве таких родоначальников о&ь являются ЗАБЫТЫЕ римско-греческие или александрийский символы. Сегодня неизвестные.
Известный русский историк математики В. В. Бобынин писал: «ИСТОРИЯ НАШИХ ЦИФР ПРЕДСТАВЛЯЕТ НЕ БОЛЕВ КАК РЯД ПРЕДПОЛОЖЕНИЙ, ПЕРЕМЕЖАЮЩИХСЯ ПРОИЗВОЛЬНЫМИ ДОПУЩЕНИЯМИ, производящими иногда, вследствие предшествующего употребления метод внушения, впечатление КАК БЫ ЧЕГО-ТО ДОКАЗАННОГО». Цит. по [989], с 53. Авторы Энциклопедии [989], после изложения различных теорий происхождения арабских цифр делами следующий многозначительный вывод: «Таким образом, МЫ ДО СИХ ПОР НЕ ИМЕЕМ ИСТОРИЧЕСКИ ОБОСНОВАННОЙ ГИПОТЕЗЫ, КОТОРАЯ ДОСТАТОЧНО УДОВЛЕТВОРИТЕЛЬНО ОБЪЯСНЯЛА БЫ ПРОИСХОЖДЕНИЕ НАШИХ ЦИФР» [989], с. 52.
Нам представляется, что дело не такое уж и сложно. Стоит лишь отрешиться от неправильных скалигеровских датировок, как происхождение «арабских цифр» становится почти очевидным. И весьма естественным. Как мы сейчас покажем, ВСЕ «АРАБСКИЕ ЦИФРЫ» ПРОИЗОШЛИ ИЗ ПРЕДШЕСТВУЮЩЕЙ ПОЛУПОЗИЦИОННОЙ СЛАВЯНО-ГРЕЧЕСКОЙ СИСТЕМЫ СЧИСЛЕНИЯ. Причем ясно будет видно, что был использован именно СЛАВЯНСКИЙ ВАРИАНТ букв-символов. Источником послужила русская скоропись XVI века. ПРОИЗОШЛО ВСЕ ЭТО, СКОРЕЕ ВСЕГО, В XVI ВЕКЕ. То есть как раз в эпоху изобретения нуля и позиционной системы счисления. Перейдем к подробному изложению.
До изобретения позиционной системы счисления и арабских цифр на Руси использовалась полу позиционная система, где для каждой десятичной цифры имелось три различных знака, в качестве которых выступали церковно-славянские буквы кириллицы [782], вып. 1, с. 16. Одна буква предназначалась для изображения данной цифры в разряде единиц. Другая — для изображения той же цифры в разряде десятков. И наконец, третья — в разряде сотен, рис. 62. Ноль отсутствовал, но, поскольку в разных разрядах обозначение цифр было разным само обозначение цифры указывало на разряд, в котором она стоит. С помощью такой системы можно было производить все обычные арифметические действия с целыми числами в пределах от единицы до тысячи. Для чисел больше тысячи приходилось применять специальные дополнительные значки, рис. 62.
Рис. 62. Старая славяно-греческая полу позиционная система записи цифр. Взято из [782], вып. 1, с. 16
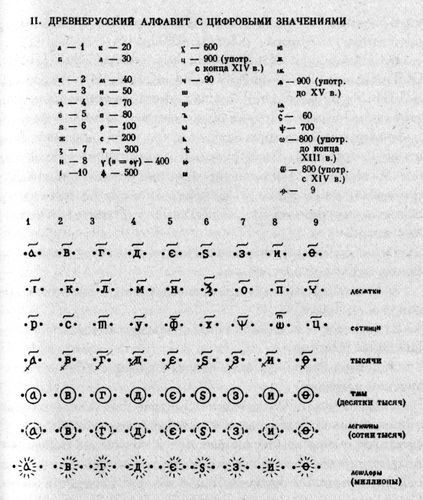
Поясним таблицу на рис. 62. Например, цифра «один» изображалась тремя способами:
1) буквой А, если единица стояла в разряде единиц, то ее в первом разряде;
2) буквой I, если единица стояла в разряде десятков, то есть во втором разряде;
3) буквой Р, если единица стояла в разряде сотен, то есть в третьем разряде.
Скажем, число РА означало 101. В нынешней позиционной системе при записи числа 101 используется ноль, так как отсутствует цифра во втором разряде. В старой же славянской полу позиционной записи нуля не было, но само обозначение единицы разными буквами указывало, что последняя из них стоит в первом, а первая — в третьем разряде. Таким образом для записи целых чисел от единицы до тысячи использовалось не ДЕСЯТЬ символов, как сегодня — ДЕВЯТЬ ЗНАЧАЩИХ ЦИФР И НОЛЬ, — а ДВАДЦАТЬ СЕМЬ букв кириллицы. НА КАЖДУЮ ЗНАЧАЩУЮ ЦИФРУ ПРИХОДИЛОСЬ ТЕМ САМЫМ ПО ТРИ БУКВЫ. В таблице на рис. 62 двадцать семи кириллических букв расположены в трех верхних строках. Под каждой арабской цифрой мы видим три различные буквы кириллицы. Остальные четыре строки таблицы на самом деле повторяют первую строку, но снабжены специальными дополнительными символами, чтобы обеспечить следующие разряды от тысячи до миллиона. Новые буквы при этом не используются.
Зададимся вопросом. Что должно было произойти, когда указанную старинную систему обозначений решили заменить на нынешнюю позиционную систему с нулем? Для этого нужно было оставить вместо двадцати семи знаков всего лишь девять (и добавить ноль). Самый простой и естественный способ — оставить из трех обозначений-букв для каждой цифры только одну кириллическую букву.
Оказывается, именно это и было сделано. Как мы сейчас увидим, в результате получились привычные нам сегодня «арабские цифры». Что сразу же делает очевидным тот факт, что люди, впервые придумавшие «арабские цифры», пользовались до этого именно славяно-греческой полу позиционной системой счисления. Причем для «арабских цифр» были использованы во многих случаях именно РУССКИЕ СКОРОПИСНЫЕ формы XVI века кириллических букв. Что может означать лишь одно. Для изобретателей арабских цифр русская СКОРОПИСЬ XVI ВЕКА была хорошо знакомым, привычным почерком.
В частности, исчезает и «великая загадка» скалигеровской истории — откуда же взялись «арабские цифры»? Они произошли из славяно-греческих цифр-букв в формах русской скорописи XVI века. Кроме того, и другие детали, о которых мы ниже расскажем, однозначно показывают, что использовалась именно РУССКАЯ, а не ГРЕЧЕСКАЯ азбука XVI века. Эти азбуки несколько отличаются.
Обратимся теперь к таблице на рис. 63. Обсудим каждую Цифру отдельно.
ЕДИНИЦА. Из трех возможных обозначений единицы была выбрана буква I (единица в разряде десятков) как наиболее простая из трех. Она обведена кружком на рис. 63. Получилась «индо-арабская» единица.
ДВОЙКА. Для двойки была использована не буква В (то есть вторая буква греческой азбуки), а буква Б — вторая буква ЦЕРКОВНО-СЛАВЯНСКОЙ азбуки. При этом была взята скорописная форма этой буквы, перевернута и зеркально отражена, рис. 63. Получилась привычная нам сегодня «индо-арабская» двойка. В данном случае автор новых обозначений явно доказал свое предпочтение славянской азбуке перед греческой, в греческой азбуке буквы Б нет. Она пропущена, и сразу после А идет В.
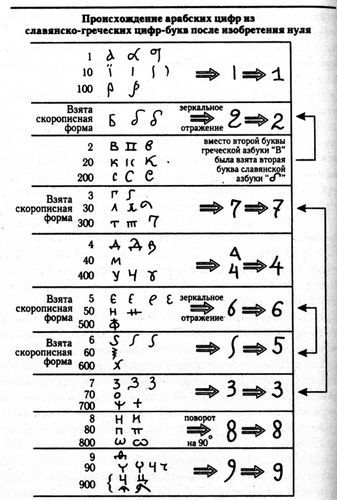
Рис. 63. Наша схема происхождения арабских цифр из славянских цифр-букв предшествующей полу-позиционной системы счисления. Обратите внимание, что во многих случаях ДЛЯ АРАБСКИХ ЦИФР БЫЛИ ВЗЯТЫ РУССКИЕ СКОРОПИСНЫЕ ФОРМЫ КИРИЛЛИЧЕСКИЕ БУКВ
Тройку мы пока пропустим, так как ее обозначение переставлено с семеркой.
ЧЕТВЕРКА. У четверки есть две формы: открытая и закрытая. Закрытая форма «домиком» получается из славянской буквы Д обозначавшей четверку в первом разряде. Открытая же форма получается из славянской буквы У, обозначавшей четверку в третьем разряде, рис. 63. Получилась «индо-арабская» четверка
Пятерку, шестерку и семерку мы пока пропустим, так как их обозначения переставлены. Подробнее об этом ниже.
ВОСЬМЕРКА. Она получается из славянской буквы «омега», обозначавшей восьмерку в третьем разряде. Буква повернута на девяносто градусов, рис. 63. Получилась «индо-арабская» восьмерка
ДЕВЯТКА. Здесь для «индо-арабской» цифры была использована нестандартная, ЧИСТО РУССКАЯ форма девятки в третьем разряде. Обычно в славяно-греческих обозначениях для этого использовалась буква Ц. Однако на Руси использовали также букву Я для обозначения девятки в третьем разряде. Мы видим, что ее скорописная форма — это в точности «индо-арабская» девятка с приделанной палочкой. Палочку отбросили. Получилась хорошо знакомая нам сегодня «индо-арабская» цифра девять, рис. 63. Упомянутая скорописная форма буквы Я была с небольшими изменениями канонизирована во время Петровской реформы и используется до сих пор. На рис. 64 приведен образец Русской скорописи начала XVII века [791], вып. 19, форзац. Здесь написано русское слово «знамя». В его конце стоит буква Я.
Перейдем теперь к «индо-арабским» цифрам: ТРОЙКА, Пятерка, шестерка и семерка.

Рис. 64. Скорописная форма славянской буквы Я в конце слова «знамя». Ясно видно, что если отбросить верхнюю палочку, то получится «ИНДО-АРАБСКАЯ» ДЕВЯТКА. Взято из [791], вып. 19

Рис. 65. Скорописная форма славянской буквы Т в начале слова. Ясно видно, что это в точности «ИНДО-АРАБСКАЯ» СЕМЁРКА. Взято из [791], вып. 19
ТРОЙКА и СЕМЁРКА. Для «индо-арабской» тройки была использована русская скорописная форма буквы 3, обозначавшая семерку в первом разряде, рис. 63. Формы русско скорописной буквы 3 и «индо-арабской» тройки полностью идентичны. И наоборот, для «индоевропейской» семерки была использована скорописная форма русской буквы Т, обозначающая тройку в третьем разряде, рис. 65. Таким образом, обозначения для тройки и семерки были почему-то ПЕРЕСТАВЛЕНЬ местами.
ПЯТЕРКА и ШЕСТЕРКА. Для «индо-арабской» пятерке была использована скорописная форма русской буквы «зело», обозначавшая шестерку в первом разряде, рис. 63. И наоборот для «индо-арабской» шестерки была использована скорописная форма славянской буквы Е, обозначавшей пятерку в первом разряде. Эта форма, кстати, очень близка к современна форме рукописной буквы Е. Создатели «индо-арабских» цифр просто зеркально отразили славянскую букву Е и получили шестерку. На рис. 66 приведен образец русской скорописи начала XVII века, где буква Е в конце слова «великие» написан как зеркально отраженная шестерка [787], вып. 7. Таким образом, обозначения для пятерки и шестерки были почему-то ПЕРЕСТАВЛЕНЫ местами. Как и в случае тройки и семерки.

Рис. 66. Скорописная форма славянской буквы Е в конце слова «великие». Ясно видно, что это в точности «ИНДО-АРАБСКАЯ» ШЕСТЕРКА получается из этой буквы Е зеркальным отражением. Взято из [787], вып. 7
НОЛЬ. Вопрос о НУЛЕ особенно интересен. Поскольку именно изобретение нуля позволило ввести НОВУЮ СИСТЕМУ СЧИСЛЕНИЯ. В современной системе счисления ноль обозначает место ОТСУТСТВУЮЩЕЙ ЦИФРЫ в том или ином разряде. Вместо нее ставится ноль. Зададимся вопросом: откуда произошло обозначения нуля привычным ныне кружочком? Старые обозначения обычно не были совсем отвлеченными, поэтому, скорее всего, обозначение нуля явилось сокращением (или видоизменением) какого-то осмысленного слова. Зададимся вопросом: какого именно? Оказывается, это легко и естественно объясняется в предположении, что исходное слово было славянским. Как сообщает В. И. Даль, слово или предлог О в русском языке раньше могло употребляться вместо приставки ОТ [223], т. 2, столбец 1467. Приставка же ОТ означает ОТСУТСТВИЕ. Этимологический словарь: ОТ — «глагольная приставка — обозначает прекращение, завершение действия; удаление, устранение чего-либо» [955], т. 1, с. 610. Таким образом, отсутствующую цифру вполне естественно было обозначить символом, похожим на букву О. По-видимому, именно так и возник современный знак нуля — кружочек «0». Что касается самого слова НОЛЬ, то оно могло произойти от старого русского НОЛИ или НОЛЬНО. Сегодня это слово уже забыто, но раньше оно часто использовалось в русском языке. Об этом говорят многочисленные примеры его употребления в старых текстах, приведенные в Словаре русского языка XI–XVII веков [789], с. 420–421. Слово НОЛЬНО, или НОЛЬНЫ, НОЛЬНЕ, НОЛЬНА использовалось, в частности, как ограничительная частица, в смысле «не прежде чем, только когда» [789], с. 421. Но ведь и ноль в десятичной записи числа можно рассматривать, как ограничительный знак, «не пускающий» цифру соседнего разряда на место отсутствующей цифры данного разряда. Дело в том, что в предшествующей славяно-греческой полу позиционной системе счисления при отсутствии значащей цифры в том или ином разряде цифры соседних разрядов придвигались друг к другу, занимая пустые места отсутствующей цифры. Именно поэтому приходилось обозначать одни и те же цифры в разных разрядах разными буквами — чтобы различить их. В позиционной же системе не нужно, поскольку на место отсутствующей значащей цифры другие цифры попасть не могут — их «не пускает» ноль. Итак, ноль могли первое время рассматривать как «не пускающий» знак, а значит, и его название вполне могло произойти от ограничительной частицы НОЛЬНО в старом русском языке. Нольно — ноль.
Кроме того, слово НОЛИ в старом русском языке употреблялось также и для обозначения не осуществившейся возможности: «помышлялъ есмь въ себе:…ноли буду лучии тогда, но худъ есмь и боленъ» [789], с. 420. В современном переводе: думал про себя: может быть, («ноли») буду лучше тогда, [но это не осуществилось], я плох и болен. Этот смысл старого слоя НОЛИ тоже весьма подходил для нуля в позиционной системе. Ведь цифра ноль обозначает как бы не осуществившуюся можность иметь значащую цифру в данном разряде.
Итак, название новой цифры НОЛЬ, позволившей ввести новую для своего времени позиционную систему счислен возникло, скорее всего, на основе именно русского языка. Та же как и новые обозначения «индо-арабских» цифр появились в результате легкого видоизменения старых русских цифр-букв. Все это происходило, как мы выяснили, не так уж давно — скорее всего, не ранее конца XVI века. А не в далеком Средневевье, как ошибочно утверждает скалигеровская хронология.
В заключение отметим, что в принципе можно пытаться искать буквы, похожие на «индо-арабские» цифры, и в других азбуках. Однако важно подчеркнуть, что для выяснения происхождения «индо-арабских» цифр подходит ДАЛЕКО НЕ ВСЯКАЯ АЗБУКА. Ведь требуется найти не просто какие-то буквы, «похожие на цифры» (что иногда удается), а буквы-цифры, ДЕЙСТВИТЕЛЬНО ИСПОЛЬЗОВАВШИЕСЯ В СРЕДНИЕ ВЕКА В КАЧЕСТВЕ ОБОЗНАЧЕНИЙ ЦИФР. Причем в силу естественной консервативности обозначений цифровые значения старых цифр-букв должны в основном сохраняться и в новой системе счисления. Как это имеет место для славянско-греческой азбуки и «индо-арабских цифр». Азбуки же, не использовавшиеся для обозначения цифр, привлекать не имеет смысла.
С нашим выводом о том, что ноль был изобретен только в конце XVI века, прекрасно согласуется и следующий известный исторический факт, поразительный с точки зрения скалигеровской хронологии. Напомним, что историки предлагают нам Рсчитать, что ноль был известен еще в глубокой древности. Однако в то же время известно, что математики даже в XVI веке ещё НЕ РАССМАТРИВАЛИ КОРНИ УРАВНЕНИЙ, РАВНЫЕ НУЛЮ [219], с. 153. Кроме того, как сообщают историки науки, естественная идея — оставить в правой части уравнения НОЛЬ, появилась лишь в конце XVI — начале XVII века [219], с 153. Хотя, повторяем, ноль по мнению историков, был к тому времени якобы уже давным-давно известен. Цитируем: «Идея приравнивания уравнения нулю БЫЛА ЧУЖДА МАТЕМАТИКЕ ВОЗРОЖДЕНИЯ. ВПЕРВЫЕ КАНОНИЧЕСКУЮ ФОРМУ УРАВНЕНИЯ привел англичанин Т. Гэрриот (1580–1621) в книге „Применение аналитического искусства“» [219], с 153.
5.3. Явные следы переделки шестерки в пятерку на старых документах
Обратимся, например, к известной гравюре «Меланхолия» знаменитого средневекового художника Альбрехта Дюрера, жившего якобы в 1471–1528 годах, рис. 67.

Рис. 67. Гравюра А. Дюрера «Меланхолия». Взято из [1232]
В правом верхнем углу гравюры нарисован так называемый магический квадрат размером 4 на 4 (четыре строки и четыре столбца). Напомним, что сумма чисел, стоящих в каждой строке, и сумма чисел, стоящих в каждом столбце магического квадрата, одна и та же. В данном случае она равняется 34. На рис. 69 мы приводим увеличенное изображение этого квадрата. А на рис. 69 показано увеличенное изображение первой клетки во втором ряду. Тут стоит цифра 5. И она Действительно ДОЛЖНА здесь стоять — иначе квадрат перестанет быть «магическим».

Рис. 68. Фрагмент гравюры A. Дюрера «Меланхолия» с изображением «магического квадрата». Взято из [1232]
Но достаточно вглядеться в изображение, чтобы стало совершенно очевидно, что эта пятерка получилась ИСПРАВЛЕНИЕМ стоявшей тут раньше цифры ШЕСТЬ, рис 69. Картина становится ясна. Нынешнюю ШЕСТЕРКУ первоначально, то есть в эпоху XVI века, использовали как обозначение цифры пять. И наоборот, нынешнюю ПЯТЕРКУ — как обозначение цифры шесть, В этих старых, первоначальных обозначениях и был нарисован «магический квадрат» Дюрера. Но когда обозначения поменялись, в новых обозначениях квадрат перестал быть магическим. Пришлось переправить рисунок. Может быть, это сделал сам Дюрер. А может быть — кто-то другой, уже после его смерти. Вероятно, переделке подверглись цифры не только на гравюрах Дюрера Но на его гравюре «Меланхолия» сохранились совершенно отчетливые СЛЕДЫ ЭТОЙ ПЕРЕДЕЛКИ ЦИФР В XVI–XVII ВЕКАХ.
Рис. 69. Откровенно переделанная цифра в «магическом квадрате» гравюры A. Дюрера «Меланхолия». Цифру 6 переделали в цифру 5. Взято из [1232]

5.4. Переделка старых дат в XVII веке
То обстоятельство, что в начале XVII века значения «индо-арабских» цифр еще не устоялись, по-видимому, было затем использовано скалигеровскими историками для фальсификации дат, относящихся к началу XVII века. Пусть в каком-то документе некоторая дата начала XVII века, например, ТЫСЯЧА ШЕСТЬСОТ ЧЕТЫРНАДЦАТЫЙ ГОД была записана по-старому, то есть как 1514 год, где символ 5, в виде буквы ЗЕЛО, обозначал цифру ШЕСТЬ. Затем цифровое значение этого символа изменилось и стало ПЯТЬ. Если забыть, что цифровое значение символа 5 менялось, то теперь дату 1514 год мы прочтем «по-новому»: как ТЫСЯЧА ПЯТЬСОТ ЧЕТЫРНАДЦАТЫЙ ГОД. Вместо подлинного исходного значения — тысяча шестьсот четырнадцатого года. Как мы видим, дата удревyилась на СТО ЛЕТ. Тем самым таким простым приемом можно было опустить вниз во времени даты многих старых документов начала XVII века. По-видимому, скалигеровские историки XVII–XVIII веков этим «методом» широко пользовались. В результате они отодвинули в прошлое лет на сто многие события XVI–XVII веков. И в самом деле, мы уже хорошо знакомы столетним хронологическим сдвигом в европейской и, в частности, русской истории.
Не исключено, что перестановка цифровых значений «индо-арабских» цифр-букв — пятерку поменяли с шестеркой, а тройку с семеркой — была отнюдь не случайной. Вероятно, преследовали цель — СКРЫТЬ ПРОИСХОЖДЕНИЕ «индо-арабских» цифр-букв из прежних славяно-греческих обозначений. Скорее всего, это происходило уже в эпоху распада Великой = «Монгольской» Империи, то есть в первую половину XVII века. Когда в Западной Европе начали писать «новую историю» не только далеких веков, но и совсем недавнего прошлого. В нашей книге «Библейская Русь» мы уже высказали мнение о том, что одним из пунктов западноевропейской государственной программы независимости было, вероятно, создание новых языков, новых правил чтения и т. п. Немаловажное место в ряду этих реформаторских мероприятий было, по-видимому, преднамеренное искажение прежней системы цифровых обозначений. Стремились отделиться от традиций прежней Великой = «Монгольской» Империи не только в языковом и культурном отношении, но и в «цифровом» тоже. Для этого переставили обозначения цифр ПЯТЬ и ШЕСТЬ, ТРИ и СЕМЬ. В результате связь старых церковно-славянских цифр-букв с новыми «арабскими» цифрами стала не так сильно бросаться в глаза. Чтобы ее обнаружить, потребовалась определенная работа. А без таких перестановок она была бы очевидной — хотя бы на примере ТРОЙКИ, которая АО СИХ ПОР ПИШЕТСЯ НЕОТЛИЧИМО ОТ СЛАВЯНСКОЙ БУКВЫ 3.
Надо сказать, что из обнаруженного нами факта еще не следует, что «индо-арабские» цифры были придуманы именно на Руси. Очень может быть, что их придумали, например, в Египте или Западной Европе в конце XVI — начале XVII века. В те годы Великая Империя была еще единой, но в одних её местах в большей степени развивалось кораблестроение, в других — наука, в-третьих — изящные искусства, в-четвертых — медицина. Все достижения и открытия становились достоянием царского Двора Империи, «шли в общий котел». В каком-то смысле владельцем всех плодов интеллектуальной, производственной и прочей деятельности считался царь-хан, император. После раскола Империи прежняя идея соревнования за лучшие достижения в расчете заслужить милость царя-хана превратилась в идею саморекламы, столь развитую сегодня в Западной Европе: наша наука, наша медицина и т. п. — самая лучшая, а сами мы — самые достойные и хорошие. Понятно, почему подобная идея самовосхваления, постоянного ревнивого сравнения себя с окружающими развилась именно в Западной Европе, а, не скажем, на Руси. Европа была далеко от метрополии Империи и в XV–XVI веках находилась в довольно затруднительном положении. Заслужить милость царского двора было для европейцев зачастую не просто стремлением выслужиться перед властью, а борьбой за существование в прямом смысле слова В ход шли все средства.
По-видимому, «индо-арабские» цифры вошли во всеобщее употребление и, в частности, в делопроизводство в Западной Европе в XVII веке. И вскоре после этого, в эпоху Петра I, были приняты и на Руси. Здесь нужно отделять этап ИЗОБРЕТЕНИЯ «индо-арабских» цифр в конце XVI — начале XVII века и этап их широкого ВНЕДРЕНИЯ. Последнее происходило уже в XVII веке, ПОСЛЕ РАСКОЛА ИМПЕРИИ, когда русское общество бывшей метрополии усилиями западных ставленников — Романовых было разгромлено и поставлено в культурную зависимость от Западной Европы. Поэтому в новой романовской России «арабские» цифры были приняты именно в том виде, в каком они НЕЗАДОЛГО ДО ТОГО начали употребляться в Западной Европе.
Но если, как мы видим, «индо-арабские» цифры были внедрены лишь в начале XVII века, а в своем окончательном виде где-то в середине XVII века, то, следовательно, все записи, использующие «индо-арабские» цифры в их современном виде, нельзя датировать эпохой ранее конца XVI века. Если нам сегодня говорят, что на некоем документе современником поставлена дата в форме 1250 год, или 1460 гол, или даже 1520 год, то это ПОДДЕЛКА. Либо подделан документ, либо подделана дата (то есть проставлена задним числом). А в случае дат якобы XVI века, как мы уже говорили, вероятно, некоторые из них относятся на самом деле к СЕМНАДЦАТОМУ веку. Сегодня их неправильно воспринимают, считая символ пятеркой, как теперь, а не ШЕСТЕРКОЙ, как было первоначально.
Б связи с этим следует заново вернуться к вопросу когда на самом деле жили известные нам сегодня деятели XV–XVI веков? Например, нас уверяют, будто знаменитый художник Альбрехт Дюрер жил в 1471–1528 годах. Усомнимся в этом. Скорее всего, на самом деле он жил в конце XVI — в начале XVII века. Поскольку старый смысл дат вида 15(…) год, проставленных на его картинах и рисунках, был, вероятно, 16(…) год. А, следовательно, и его известные гравюры, звездные карты к птолемеевскому Альмагесту и т. д., были изготовлены не в начале XVI века, как нам сегодня говорят, а в начале XVII века. Напомним, что наш анализ Альмагеста показал, что эта книга в своем современном виде появилась, скорее всего, не ранее начала XVII века См. нашу книгу «Астрономический анализ хронологии». А, следовательно, и дюреровские звездные карты к Альмагесту были изготовлены примерно в это же время. А не на 100 лет раньше.
Приведем теперь несколько примеров записи дат на старых картинах и рисунках нескольких известных художников Средневековья. После всего сказанного выше становится понятным, что эти работы следует датировать ПРИМЕРНО СТА ГОДАМИ ПОЗЖЕ, чем это принято считать сегодня.

Рис. 70. Автопортрет A. Дюрера, датируемый якобы 1493 годом. На самом деле это, скорее всего, 1593 год. То есть на сто лет ближе к нам. Взято из [1232], картина № 1
На рис. 70 приведен автопортрет А. Дюрера [1232], картина 1. Над головой художника крупно проставлена дата, рис. 71. Сегодня считается, что здесь написан 1493 год. Однако обратим внимание на форму второй слева цифры, якобы четверки. Не получена ли она путем легкого искажения славянской буквы «есть»? То есть прежней старой ПЯТЕРКИ. Если это так, то дата на автопортрете Дюрера окажется другой — 1593 год. То есть самый конец ШЕСТНАДЦАТОГО ВЕКА, на 100 лет позже чем принято думать сегодня.
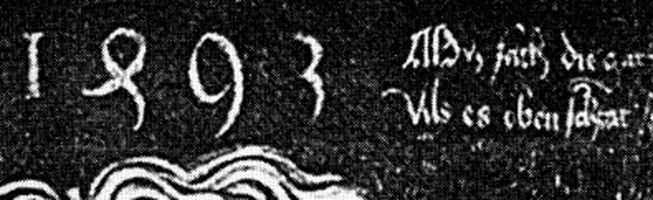
Рис. 71. Увеличенный фрагмент с датой на автопортрете А. Дюрера
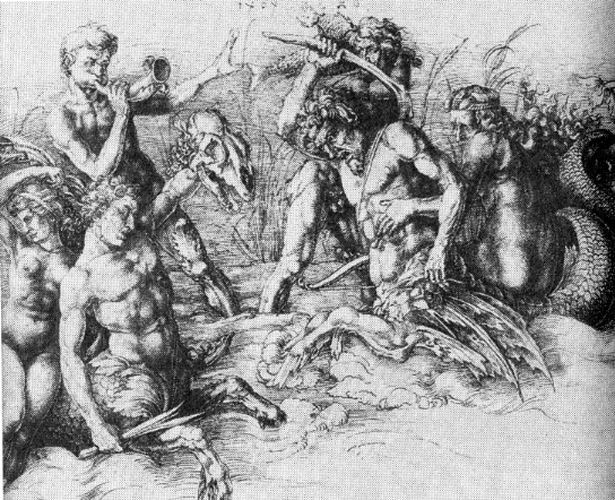
Рис. 72. Гравюра А. Дюрера «Битва морских богов». Наверху проставлена дата якобы 1494 год. На самом деле это скорее всего 1595 год. То есть, на сто лет ближе к нам. Взято из [1232], № 4
На рис. 72 приведена одна из гравюр А. Дюрера [1232] номер 4. Наверху проставлена дата,
Рис. 73. Увеличенный фрагмент с датой на гравюре А. Дюрера «Битва морских богов». Взято из [1232], № 4

Нам говорят, что тут стоит 1494 год. Однако всмотримся внимательнее в так называемую «четверку». Она написана практически так же, как и славянское рукописное Е. То есть как ПЯТЕРКА в старых обозначениях. Если это так, то данный рисунок А. Дюрера датируется не 1494 годом, а 1595 годом — концом XVI века.

На рис. 74 приведена картина А. Дюрера [1232], номер 11. На ней проставлена дата, Рис. 74 Картина А. Дюрера, датируемая якобы 1499 годом. На самом деле это, скорее всего, 1599 год. То есть на сто лет ближе к нам. Взято из [1232], № 11
Рис. 75. Фрагмент с датой на картине A. Дюрера якобы 1499 года
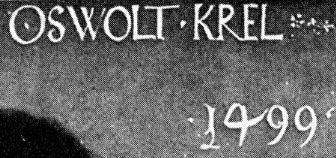
Сегодня считается, что это 1499 год. Однако опять-таки здесь мы видим «четверку», которая является просто повернутой славянской буквой Е. Вероятно, здесь стоит ПЯТЕРКА в старых обозначениях, и, следовательно, эта картина датируется не 1499 годом, а 1599 годом. То есть концом XVI века.

На рис. 76 приведена гравюра А. Дюрера [1232], номер 12. Рис. 76. Рисунок А. Дюрера, датируемый якобы 1502 годом. На самом деле это, скорее всего, 1602 год. То есть на сто лет ближе к нам. Взятою [1232], № 12
На ней, внизу, проставлена дата, рис. 77.Рис. 77. Фрагмент с датой на рисунке А. Дюрера, датируемом якобы 1502 годом

Считается, что это 1502 год. Однако, как мы объяснили выше, скорее всего, здесь символ 5 обозначает ШЕСТЕРКУ. Следовательно, это 1602 год — начало XVII века, на 100 лет позже, чем считается сегодня. Кстати, такая великолепная техника исполнения рисунка, как теперь становится понятно, возникла лишь в XVII веке.

На рис. 78 приведена картина А. Дюрера [1232], номер 16. Над головой женщины, изображенной на картине, проставлена дата, датируемая якобы 1505 годом. На самом деле это, скорее всего, 1606 год. То есть на сто лет ближе к нам. Кроме того, первая цифра «один» записана явно как кириллическое Х то есть — как первая буква имени Христос. Взято из [1232], № 16
Рис. 79. Фрагмент с датой на картине А. Дюрера, датируемой якобы 1505 годом
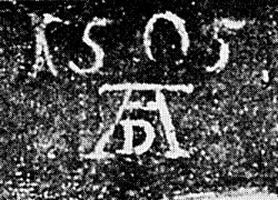
Сегодня нас уверяют, будто это, очевидно, 1505 год. Но в свете того, что нам теперь стало известно, это, скорее всего, 1606 год, поскольку старое цифровое значение символа 5 было ШЕСТЬ. Кроме того, в этой дате первая единица обозначена буквой X, а не буквой I, рис. 79. Но ведь буква X — это первая буква имени Христос. Это в точности отвечает нашей мысли, что в начале даты раньше ставили первую букву имени Иисус или имени Христос!
И лишь потом эту букву объявили обозначением «тысячи». Между прочим, в данном случае, на картине А. Дюрера, буква X в дате записана в форме характерной именно для КИРИЛЛИЦЫ.
Все сказанное относится отнюдь не только к Альбрехту Дюреру, но и ко всем художникам и скульпторам, на картинах которых стоят даты якобы XV–XVI веков. Это относится и к датам, проставленным на старых книгах. В том числе и на первопечатных.

На рис. 80 приведена картина Ганса Фриза «Усекновение головы Иоанна Крестителя» из Базельского художественного музея [104], номер 10. Внизу проставлена дата, рассматриваемая сегодня как 1514 год, рис. 81. Однако, как мы уже объяснили, старое цифровое значение символа 5 было ШЕСТЬ. Так что, скорее всего, это 1614 или 1615 год. Обратим также внимание на запись первой цифры «один». Это явное «И с точкой», то есть i. Кроме того, впереди поставлена еще одна точка. Итак, в качестве «первой цифры» мы видим I, то есть первую букву, имени Icyс (в старом написании). Это в точности отвечает нашей реконструкции.

Неустойчивость форм «индо-арабских» цифр в эпоху XVI — начала XVII века ярко проявляется, например, на картинах знаменитого средневекового художника Луки Кранаха Сегодня считается, что он жил в 1472–1553 годах [797], с. 643. Например, одна и та же цифра 5 — означающая у Кранаха, скорее всего, ШЕСТЬ (а не пять, как сегодня) — НА РАЗНЫХ ЕГО КАРТИНАХ ВЫГЛЯДИТ СОВЕРШЕННО ПО-РАЗНОМУ. Как мы теперь начинаем понимать, Лука Кранах жил, скорее все-го, не в XV–XVI веках, а в XVI–XVII веках. Подобные колебания в написании цифр на его картинах указывают, что еще и в XVII веке правила написания «индо-арабских» цифр не устоялись. На рис 82 приведена гравюра Луки Кранаха Старшего «Давид и Абигайль» [1310], с. 7. Внизу справа изображена дощечка с инициалами Луки Кранаха, изображением дракона и с ДАТОЙ, рис 83.

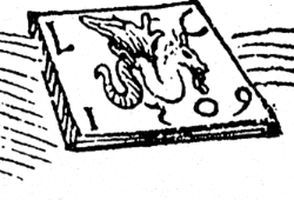
Сегодня считается, что тут написан 1509 год. На самом деле это, скорее всего, 1609 год. Обратите внимание на цифру 5, то есть на первоначальную шестерку (а не пятерку, как сегодня). Она отличается от современного написания 5 тем, что ЗЕРКАЛЬНО ОТРАЖЕНА. Кстати, стоит обратить внимание на то, как представлен здесь «древний» библейский царь Давид. Это типично средневековый рыцарь, в тяжелых латах. Рядом с женщиной Абигайль на земле, лежит ее шляпа с ПЕРЧАТКАМИ.
Таким образом, средневековый художник Лука Кранах не видел ничего странного в том, что «древняя» библейская Абигайль — это средневековая женщина, носившая, в частности, такие предметы позднесредневекового туалета, как ПЕРЧАТКИ и шляпу с полями.

Вернемся к записи дат на средневековых документах. Непривычную сегодня, ЗЕРКАЛЬНО ОТРАЖЕННУЮ ФОРМУ имеет и цифра 5 в дате на гравюре Луки Кранаха «Святой Георгий» [1258], с. 9. См. рис. 84. Сегодня нам говорят, что тут записан 1509 год. Однако, скорее всего, это 1609 год, то есть начало XVII века.
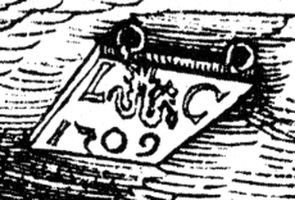
Точно такую же ЗЕРКАЛЬНО ОТРАЖЕННУЮ ФОРМУ имеет цифра 5 на гравюре Луки Кранаха якобы 1509 года, изображающей святого Иеронима [1310], с. 14. См. рис. 85. На этой гравюре дощечка с датой нарисована перевернутой вверх, ногами. Для удобства чтения мы перевернули ее обратно. Скорее всего, здесь записан 1609 год. ЗЕРКАЛЬНО ОТРАЖЕННУЮ ФОРМУ имеет цифра 5 и на гравюре Кранаха «Johannes der Taufer im Wald preligend» якобы 1516 года. Взято из [1258 | с. 35. Фрагмент гравюры с датой мы приводим на рис. 86. Скорее всего, тут записан 1616 год. Однако на некоторых других картинах ТОГО ЖЕ ЛУКИ КРАНАХА цифра 5 написана по другому. А именно как пятерка пишется сегодня. Например на его гравюре «Турнир со шпалерой» якобы 1509 года [131$ с. 8–9. Мы приводим фрагмент с датой на рис. 87. Скорее всего, эта гравюра датируется 1609 годом.

Рис. 86. Фрагмент с датой на гравюре Луки Кранаха «Johannes der Та ufer im Wald preligend», якобы 1516 года. Цифра 5 написана в зеркально отраженном виде. Взято из [1258], с. 35

Рис. 87. Фрагмент с датой на гравюре Луки Кранаха «Турнир со шпалерой», якобы 1509 года. Здесь цифра 5 написана уже так, как её пишут сегодня. Взято из [1310],с.8–9
В современном виде записана цифра 5 на картине Луки Кранаха, изображающей Ганса Лютера якобы 1527 года [1258] с 41. Мы приводим фрагмент с датой на рис. 88.

Вероятно эта картина была написана в 1627 году. То есть столетием позже, чем считается сегодня. На рис. 89 мы приводим фрагмент с датой на картине Луки Кранаха «Женский портрет» якобы 1526 года [1310], Государственный Эрмитаж, Петербург. Цифра 5 написана в современном виде. Как мы понимаем, на самом деле тут, скорее всего, записана дата 1626 год.
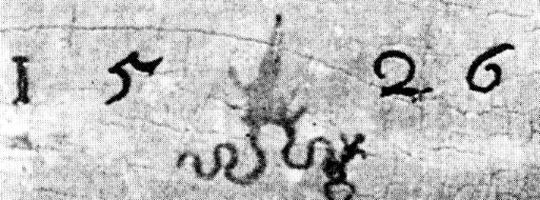
ВАЖНОЕ ЗАМЕЧАНИЕ. Сегодня, когда мы смотрим на старые гравюры XVI–XVII веков — рисунки, географические карты и т. д., - то обычно уверены, что те оттиски, которые мы видим, действительно изготовлены автором в XVI или XVII веке Однако это далеко не всегда так. Дело в том, что автор гравюры вырезал изображение на доске — медной или деревянной. С нее уже делались оттиски: в изображение на доске втиралась краска, затем излишки краски убирались так, чтобы краска оставалась лишь в углублениях, сделанных резцом гравера. Потом на доску накладывали мокрую бумагу, поверх которой клали войлок. Под большим давлением оттиск прокатывался валиком. В результате бумага с силой вдавливалась через войлок во все углубления медной доски и забирала из них краску. Получался оттиск. Важно, что оттиски могли делать и намного позже, чем была изготовлена сама доска. Гравированные медные доски не уничтожались, а переходили из рук в рук, продавались и т. д. Гравюры-оттиски со старых досок могли делать и в XVIII, и в XIX веках. При этом не составляло большого труда внести некоторые изменения в изображение. Например переделать дату на рисунке или название на карте. Для этого достаточно было лишь отшлифовать требуемое место на доске, уничтожив первоначальное изображение, и выгравировать на этом месте новое. При прокатке листа бумаги тяжелым валом через войлок, мокрый лист по-прежнему хорошо прилегала к медной доске, даже в зашлифованных (слегка углубленных) местах, образовавшихся после редактирования. В результате получался «старый знаменитый оттиск», но с некоторыми новыми деталями.
То, что так действительно происходило, хорошо известно. Например, в случае географических карт. Примеры такого редактирования мы лично видели на выставке старых географических карт в Москве в октябре 1998 года, в выставочной галерее «Юнион» на Смоленской площади. Об этом факте нам сообщили организаторы выставки, специалисты по древним картам. В частности, нам показали два оттиска старой карты с одной и той же медной доски. Один из них был сделан до редактирования, а второй, с рядом новых деталей, — после. В данном случае изменение было сделано не с целью подделки, а из чисто практических соображений — требовалось внести новые географические сведения на старую карту. Но, как мы понимаем, то же самое можно было проделать и с целью, скажем, фальсификации даты на карте. Или какого-то названия на ней. Переделать всю медную доску — большая работа. А вот внести несколько мелких, но принципиальных изменений — совсем несложно.
Фоменко .Носовский. Новая хронология